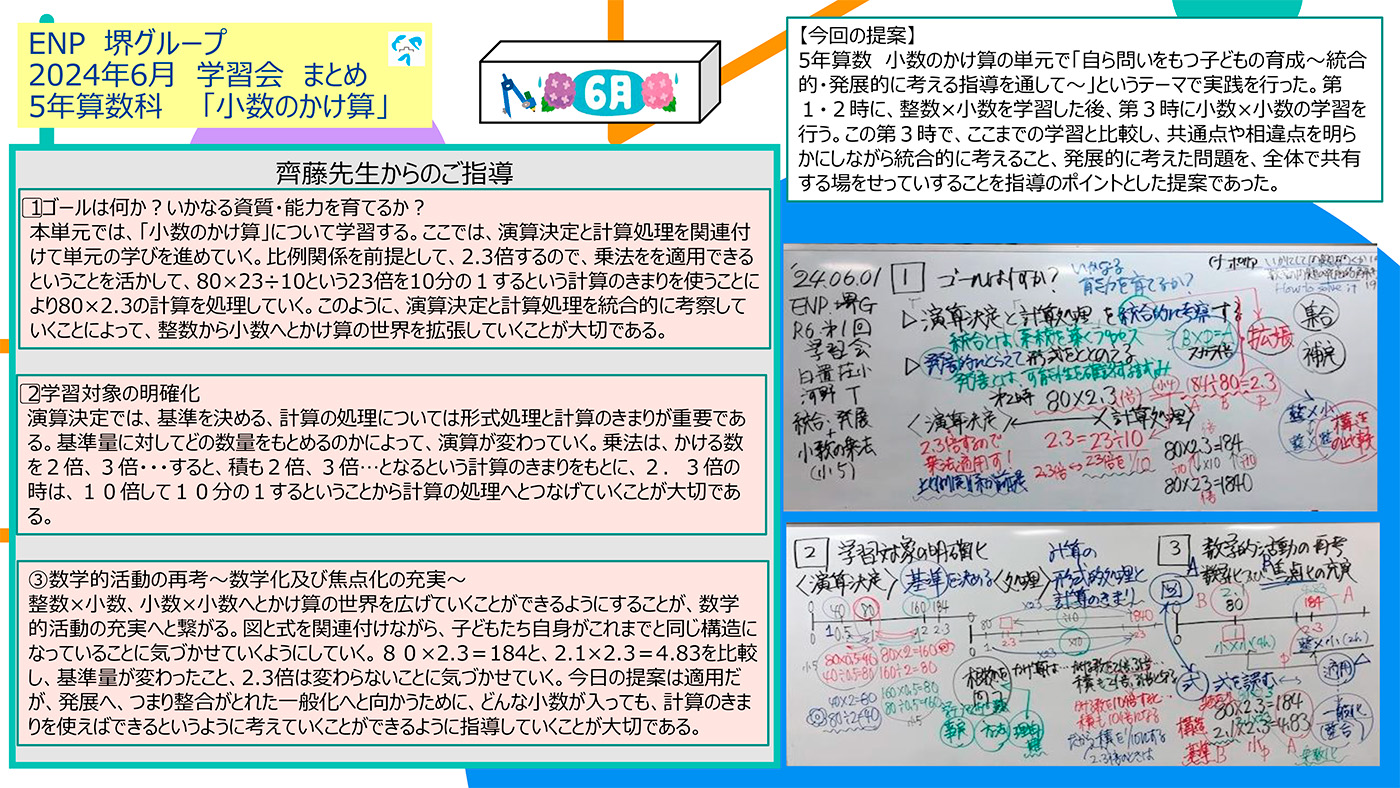
今回の提案
5年算数「小数のわり算」を通して、「比較と根拠を意識した単元展開を通して統合的に考える子を育てる」というテーマをもとにした提案であった。単元を通して、既得の数学的な見方・考え方を働かせ、新たな数学的な見方・考え方を獲得していくことができるようにしていった。特に、純小数でわることの意味を考える場面では、子どもたちが数直線図を使って試行錯誤しながらその意味を考える姿が見られるものであった。
齊藤先生からのご指導
子どもが既得の内容との整合性を問い続ける学び
基準量B(1mあたりの値段)、割合p、比較量A(代金)とする場合、乗法はB×p=A、除法とはA÷p=Bになる。学習指導要領P.239に掲載してある数直線図の関係が大事である。×0.5、÷0.5の計算は、これまで、基準量の捉え方を変えて、÷2、×2として捉えてきたから、子どもたちはこの1より小さい数でわるという立式に困難さを感じる。「どうして1より小さい数でわったら答えが答えが大きくなるの?」という問いに対して、「わり算は1mあたりの代金を求めるからある長さとその代金から求める計算。だから、比較量÷割合=基準量となり、どこを基準量と見るかによって変わってくる」というかけ算とわり算の関係の本質を捉えることができていないからである。この関係性を理解させるのは、困難だことであるため、被乗数と積、被除数と商の関係への理解に留めているのが教科書の展開となっている。困難さのあるこの教材の本質を教師自身が理解していることが大切である。
演算決定のプロセスと問い
「根拠を問う」、「整合性を問う」という視点から、「同じようにできないかな」と考えることができるようにしていきたい。「代金は比例関係を前提とした乗法で求めることができる。」という根拠をもとに、×0.5という演算決定ができるようにしていく。さらに、整数値での考えをもとに、「1mあたりの値段はわり算で求めることができる」というように類推しながら整合性を問う。ここで、乗法と除法について、新しくできるようになったことについて考えさせることで、1より小さい小数についても乗法や除法が適用できる範囲を拡張していき、乗法と除法を統合していく。そして、どんな数値でも、代金を求めるのかによって、 1mあたりを求めるのかで、乗法と除法の演算決定することができるようにしていくこで、数学らしく思考する習慣を身につけさせていく。このような指導は、乗法と除法を併進させていく単元展開を取り入れていく必要があるだろう。









