8月3日 数学的な授業を創る会(豊中)レポート
「データを活用して表現する力をそだてる」
礒野宗一郎先生の「3年 表とグラフ」実践

児童一人一人がそれぞれに見いだしたことを自己主張する活動が必要
第6学年における学習を見据え、統計的探究プロセスを第3学年から徐々に取り入れることとし、学級の生活改善を図るべく、「忘れものをなくすために」をテーマに単元を構成した。忘れ物の実態調査を提示したところから学習が始まり、その実態を表や棒グラフにまとめた。そこから疑問に思うことを基にアンケート調査やその分析を行い、忘れ物をなくすために大切にしたいことをポスターにまとめ、交流した。
<議論の柱>
6年生で統計的探究プロセスを回せるようにするために3年生でつけておくべき批判的思考とはどのような力か、どのような活動が有効なのか。
・徐々に取り入れることは必要。
・データをまとめたグラフから、どのようなことを読み取るのかという力を育てることが大切である。
・生活改善のためのデータである。「ここは分かった!」だけでなく、「ここはどうなのだろう・・・?」と、不明なところがあれば、データを取り直すことも必要。それが批判的思考につながる。
・自分たちが行ってきたことを、「これでよかったのか・・・?」と問い直すのが、批判的思考である。
齊藤一弥先生からの御指導
1【why?】「表やグラフ」を活用する(いかす)とは?
・「表やグラフ」を活用する(いかす)とは、「統計的に物事を考察する」ことである(見方・考え方の「考え方」にあたる)。※H29-CS, PP.23)
(1) 表やグラフが使える【※「知識・技能」にあたる】
・「表やグラフの意味、機能などを問題解決に生かす」ということ。表やグラフを「かける」「知っている」とは違う。
(2) 表やグラフの価値を知っている【※ 【思考力・判断力・表現力】にあたる】
・「表現のよさ、働き、必要性を問題解決に用いることができる」ということ。
・「積み上げ棒グラフ」→何がよさなのか・・・「部分と全体」を比較できるようになった。
※授業や協議の中で扱う!それが扱える文脈を!
(3) 表やグラフのよさを生かす【※「学びに向かう力」にあたる】
・新たな問題解決の見通しをもつこと。数学的にどのように扱うか、ということを分析することが大切。
2【What?】「数学的な表現」とは?
・「数学的な表現」・・・目標(H29-CS「簡潔」「明瞭」「的確」とある)、内容(「働き」「よさ」「必要性」)、方法(問題解決に生かすこと。グラフは問題解決の道具である)は3つの側面をもっている。
・中原(1995)は、構成的アプローチの研究において、5つの表現体系を示している。(※板書を参照)
①具体(現実場面)教科書の情景図など
②半具体(操作的表現) 計算ブロックの操作など
③言語テキスト(言葉。動的なもの)
④非言語テキスト(表、グラフなど。静的なもの)
⑤形式(数学の言葉=数学語や数学の文法。数と式などの規約的表現)
①から⑤に向かって抽象化される。
・今回の提案では、この③④の往還がなされるべきであった。
3【How?】「表現」のつながり>今日の提案を生かすならば・・・
・ 具体→②非言語テキスト→③言語テキスト・・・のサイクルを回すこと(今回は、グラフ以上の表現をすることにはならない)。
・「PPDAC」※大切だが、表やグラフといった「表現」は、その質を高めることが大切になる。
①具体の場面(現実場面のデータが示され、ある目的が生じる)
②非言語テキストにする(表、グラフに表す)
・表やグラフも、一種の規約的表現。「的確」
(exact=誰にでも伝わる)なものである。非言語テキストに表現にすることで、論理的思考を可能にする。
③言語テキストで具体的に表現する
・「つまり、~である。」「例えば、〜である。」など、表現を言葉で置き換える。そこに、自らの考えを入れて形成していく。
※国語「C 読むこと」 4つの指導事項・・・
〇構造と内容の把握、〇精査・解釈、〇考えの形成、〇共有)
③で形成したことは、①の目的に沿うものになっているかどうか。データの特徴や向を読むこと。
・今回、磯野先生が提案したかったことは、「数学的な表現の質を高める」こと。①②③のサイクルで、数学らしい表現を追い求めていく中で、「本当にこの表現でよいのカ」というところに、批判的思考が位置付く。批判的思考ができるようになるために、批判的思考をしていくのではない。
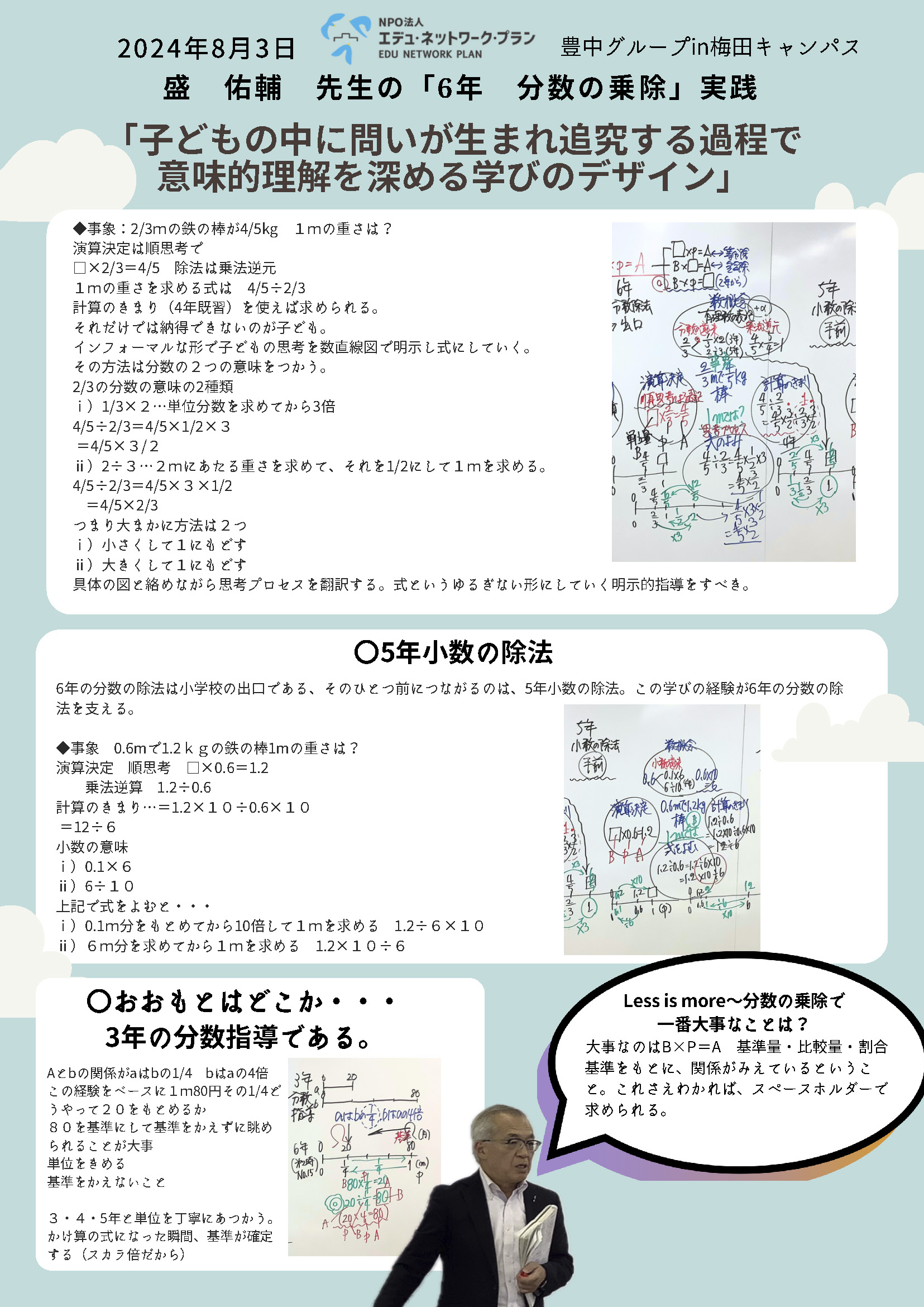
「子どもの中に問いが生まれ追究する過程で意味的理解を深める学びのデザイン」
盛 佑輔先生「6年 分数の乗除」実践

計算方法の考察に焦点を当てた単元構成にすることで、
分数の意味や性質に立ち返り意味的理解を深めることを目指す。
分数の乗法と除法を統合的に捉えられるように、単元の序盤から計算方法の考察に焦点を当てて進める。演算決定をあとで取り扱い、逆数の捉えを数量関係から見出す子どもを目指した。
<協議の柱>
計算方法の考察に焦点を当てた一つの大きな単元をつくることで児童の意味的理解が深まったか 計算の考察をした上で演算決定の場面を関連付けることで児童の意味的理解が深まったか。
この場面における意味的理解:分数の意味や計算に関して成り立つ性質と手続き的知識が結びついている 乗除法の形式を統合(補完による統合)している
・演算決定を序盤で扱わないことに違和感を持つ。
・多面的にみることより、子どもに批判的に見ることを主張されたが、結果子どもは意見が多すぎた様子
だった。その意図は?
→子どもが逆数を根拠なくひっくりかえしてかけるという手続き的に扱う姿勢ではなく、なぜ、逆数をカ
けるのかについて、その意味を子どもに熟考させたかった。色々な目の付け所で困り感を解決してく中でこそ、アイデアが生まれ、数量関係を常に捉えさせることになり、逆数をかけるという意味に迫れると考えた。
・単元構成として、最初に計算を張り付けているなら、後半のどこで問題場面を張り付けるかが大事だと感じる。せっかく数直線で抑えているのであれば、基準がずれてくるので混乱しているように感じた。
・逆数という扱いがあいまいだから明確にしたいということが提案だった。逆数のよさを感得させたかったと思うが、子どもが逆数のよさをどう感得していくの力、難しい課題である。
・乗除法の形式の統合ということは、基準量X割合=比較量、基準量みつけるときは除法とやってきた。
今までやってきたことと同じとみることが乗除法を統合することであると考える。だから、演算決定が見えたときに、逆数を使う。逆数が見えてくるはず。演算決定の取り扱いを再考。
<齊藤一弥先生からの御指導>
Less is more
〜もしたったひとつだけ分数の乗除で指導することを問われたらなんと答えますか?〜
数と計算領域で育てるべき資質・能力は?
・数概念
・計算のきあり
・演算決定
・式の表現・読み
この4つが組み合わさって整い、能力が育成される。
分数の除法では、問題解決を通しながら、数概念として分数の意味を理解させる。演算決定で除法の意味が焦点となり、計算のきまりとして除法の性質を利用し理解を深める。そして、平成29年の改訂で「式指導(式の表現と読み)」が数と計算領域に新設されたことが大事で、式は、思考プロセス。式と数直線図を往還させながら、子どもの思考と式、そして数量関係をつなぎ、理解を深めさせていくことが肝要。
計算の決まりだけで逆数にもっていっても子どもは腑に落ちない。
インフォーマルな形の式にし、量の理解にもっていかないと子どもは腑に落ちない。数直線にのせて明示的に指導することが大事。









