今回の提案
5年算数小数のかけ算の単元で「自ら問いをもつ子どもの育成~統合的・発展的に考える指導を通して~」というテーマで実践を行った。第1・2時に、整数×小数を学習した後、第3時に小数×小数の学習を行う。この第3時で、ここまでの学習と比較し、共通点や相違点を明らかにしながら統合的に考えること、発展的に考えた問題を、全体で共有する場をせっていすることを指導のポイントとした提案であった。
齊藤先生からのご指導
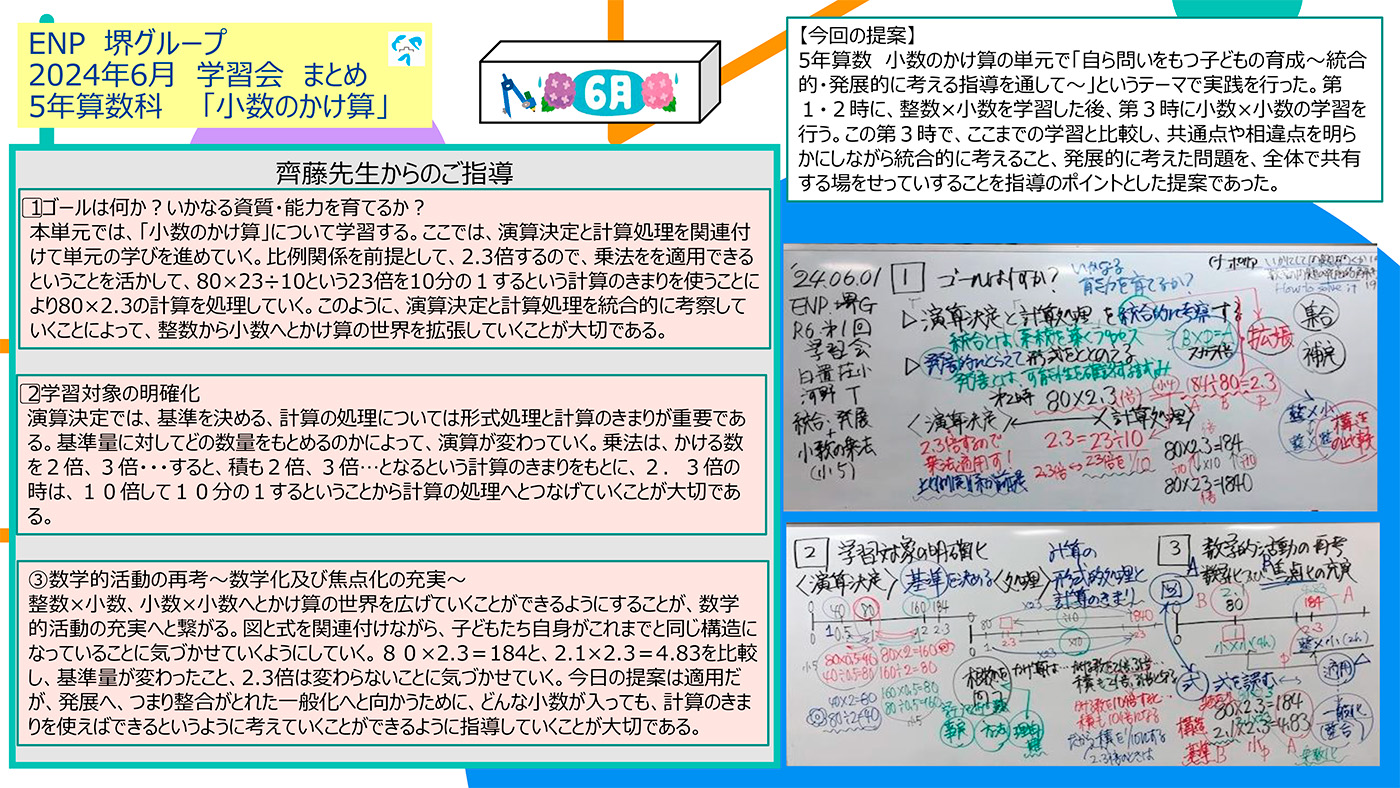
ゴールは何か?いかなる資質・能力を育てるか?
本単元では、「小数のかけ算」について学習する。ここでは、演算決定と計算処理を関連付けて単元の学びを進めていく。比例関係を前提として、2.3倍するので、乗法をを適用できるということを活かして、80×23÷10という23倍を10分の1するという計算のきまりを使うことにより80×2.3の計算を処理していく。このように、演算決定と計算処理を統合的に考察していくことによって、整数から小数へとかけ算の世界を拡張していくことが大切である。
学習対象の明確化
演算決定では、基準を決める、計算の処理については形式処理と計算のきまりが重要である。基準量に対してどの数量をもとめるのかによって、演算が変わっていく。乗法は、かける数を2倍、3倍・・・すると、積も2倍、3倍…となるという計算のきまりをもとに、2.3倍の時は、10倍して10分の1するということから計算の処理へとつなげていくことが大切である。
数学的活動の再考~数学化及び焦点化の充実~
整数×小数、小数×小数へとかけ算の世界を広げていくことができるようにすることが、数学的活動の充実へと繋がる。図と式を関連付けながら、子どもたち自身がこれまでと同じ構造になっていることに気づかせていくようにしていく。80×2.3=184と、2.1×2.3=4.83を比較し、基準量が変わったこと、2.3倍は変わらないことに気づかせていく。今日の提案は適用だが、発展へ、つまり整合がとれた一般化へと向かうために、どんな小数が入っても、計算のきまりを使えばできるというように考えていくことができるように指導していくことが大切である。









