7月14日 数学的な授業を創る会(豊中)レポート
円周率の追究で身に付けたい力は? WHY?
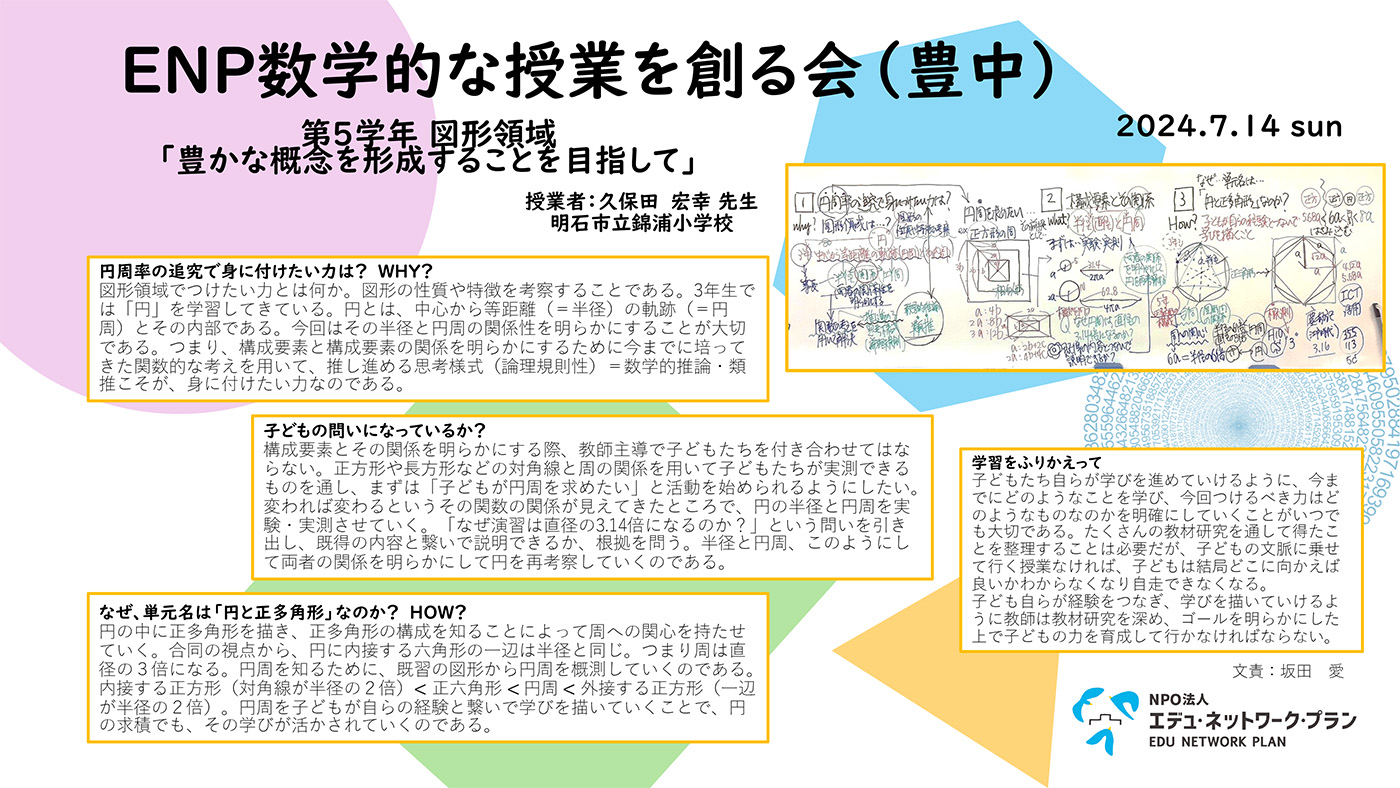
図形領域でつけたい⼒とは何か。図形の性質や特徴を考察することである。3年⽣では「円」を学習してきている。円とは、中⼼から等距離(=半径)の軌跡(=円周)とその内部である。今回はその半径と円周の関係性を明らかにすることが⼤切である。つまり、構成要素と構成要素の関係を明らかにするために今までに培ってきた関数的な考えを⽤いて、推し進める思考様式(論理規則性)=数学的推論・類推こそが、⾝に付けたい⼒なのである。
子どもの問いになっているか?
構成要素とその関係を明らかにする際、教師主導で⼦どもたちを付き合わせてはならない。正⽅形や⻑⽅形などの対⾓線と周の関係を⽤いて⼦どもたちが実測できるものを通し、まずは「⼦どもが円周を求めたい」と活動を始められるようにしたい。変われば変わるというその関数の関係が⾒えてきたところで、円の半径と円周を実験・実測させていく。「なぜ演習は直径の3.14倍になるのか?」という問いを引き出し、既得の内容と繋いで説明できるか、根拠を問う。半径と円周、このようにして両者の関係を明らかにして円を再考察していくのである。
なぜ、単元名は「円と正多角形」なのか? HOW?
円の中に正多⾓形を描き、正多⾓形の構成を知ることによって周への関⼼を持たせていく。合同の視点から、円に内接する六⾓形の⼀辺は半径と同じ。つまり周は直径の3倍になる。円周を知るために、既習の図形から円周を概測していくのである。内接する正⽅形(対⾓線が半径の2倍)< 正六⾓形 < 円周 < 外接する正⽅形(⼀辺が半径の2倍)。円周を⼦どもが⾃らの経験と繋いで学びを描いていくことで、円の求積でも、その学びが活かされていくのである。
学習をふりかえって
⼦どもたち⾃らが学びを進めていけるように、今までにどのようなことを学び、今回つけるべき⼒はどのようなものなのかを明確にしていくことがいつでも⼤切である。たくさんの教材研究を通して得たことを整理することは必要だが、⼦どもの⽂脈に乗せて⾏く授業なければ、⼦どもは結局どこに向かえば良いかわからなくなり⾃⾛できなくなる。⼦ども⾃らが経験をつなぎ、学びを描いていけるように教師は教材研究を深め、ゴールを明らかにした上で⼦どもの⼒を育成して⾏かなければならない。









