土曜日学習会一大企画がついに実現しました!昨年、東京学芸大学附属小金井小のセミナーに参加した際、加固先生の「島根に行きます!」という言葉を真に受け、計画を進めること一年、ついに小金井小の加固希支男先生、尾形祐樹先生をお招きして算数授業研修会を行うことができました。さらに、文部科学省教科調査官の笠井先生、学力調査官の直海先生も来てくださり、各藤先生含め5名の超豪華共演となりました。当日は70名の参加者と大研修会となりました。

尾形先生の授業 2年「分数」
研究主題~1/3を、子どもにどう指導するか、子どもはどう理解するか〜
2年生の子どもが、今まで操作として理解していた分数から、割合としての分数へ概念を広げていく時、どのような状態が1/3と見ることができていると言えるのか、子どもの分かっていく過程やつまずく過程を表出させていくことを狙われた。
授業では、12 マスのテープを3等分して1/3を理解することや、もとの大きさが遊っても1/3にすることができるということ、1/3はすべて同じ大きさでないといけないということ、12 このチョコレート(3X4 の分離量)を3等分すること、形が異なる1/3も1/3といえるのか、など盛り沢山の内容で、分数指導で大切にしなければならないことを実践を通して教えて頂いた。
尾形先生が算数の授業で大切にされていること
つまずいている子が、どういう所でつまずいているのかを見ていきたい。間違えちゃだめ、正解だけを見つけるものではなく、そのつまずきの中にヒントがあったり他の子の共感が生まれたりすることを大事にしている。見方・考え方(着目ポイント)を重視し、問題が解けたで終わりでなく、子どもがいつでも使える方法(一般化)を見つけていく姿を目指している。
加固先生の授業 3年「倍の計算」
研究主題〜第3学年における比例的推論を用いた問題のあり方について〜
比例的推論とは、2量の比例関係を見抜き、問題解決に活かす推論である。
リボンの長さと代金が比例関係であることを根拠に、購入したリボンの代金の求め方を考える活動を行われた。
まず、「4mで50円のリボンを12m買うと、代金は?」という「1とみる大きさが明示されている問題」を提示し、50X3を見いだした子どもに、「なぜ3倍になるの?」と根拠を問うことで、長さが3倍になると、代金も3倍になるという比例関係に子どもが番目できるように丁寧に指導された。
次に、「同じリボンを10m買うと代金は?」という「1とみる大きさを新しく考える必要がある問題」を提示し、「8mの代金は分かったけど、あと2mどうしようかな。」や「2倍もできるなら÷2もできる。」と子どもの言菜を繋いで、比例関係を根拠に問題解決していく過程を学ぶことができた。
加固先生が算数の授業で大切にされていること
一斉授業しても、全員は見取れない。本当に分かっているか、「説明してごらん。」と一人でも多く子ども自身に表現させたい。1日で全員できなくても、3日間かけて全員に表現できるようにしていくことを大切にしている。
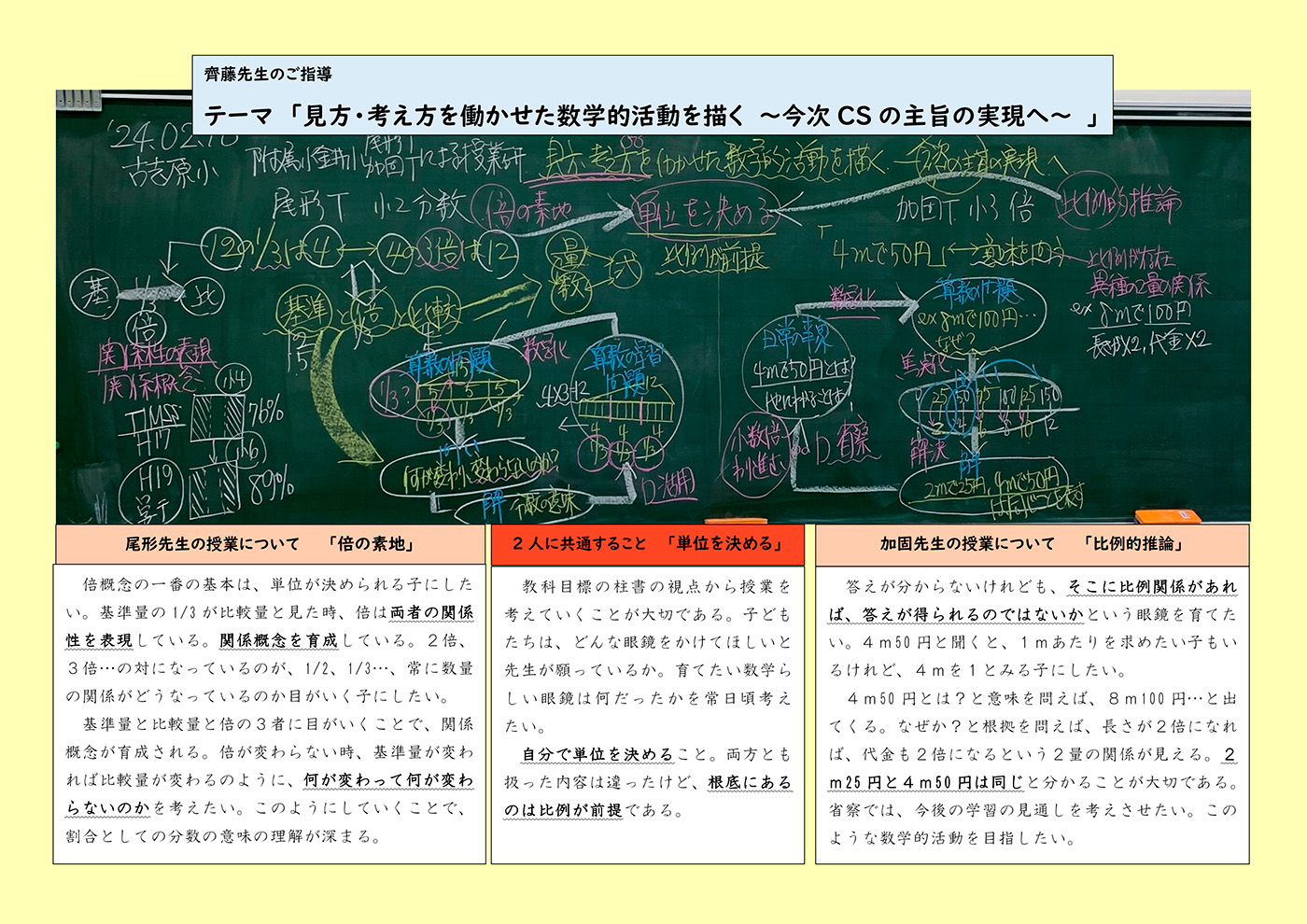
齊藤先生のご指導
「見方・考え方を働かせた数学的活動を描く〜今次 CS の主旨の実現へ〜」
尾形先生の授業について「倍の素地」
倍概念の一番の基本は、単位が決められる子にしたい。基準量の1/3が比較量と見た時、倍は両者の関係性を表現している。関係概念を育成している。2倍、3倍・・の対になっているのが、1/2、1/3…、常に数量の関係がどうなっているのか目がいく子にしたい。基準量と比較量と倍の3者に目がいくことで、関係概念が育成される。倍が変わらない時、基準量が変われば比較量が変わるのように、何が変わって何が変わらないのかを考えたい。このようにしていくことで、割合としての分数の意味の理解が深まる。
加固先生の授業について「比例的推論」
答えが分からないけれども、そこに比例関係があれば、答えが得られるのではないかという眼鏡を育てたい。4m50円と聞くと、1mあたりを求めたい子もいるけれど、4mを1とみる子にしたい。4 m50円とは?と意味を問えば、8m100円…と出てくる。なぜか?と根拠を問えば、長さが2倍になれば、代金も2倍になるという2量の関係が見える。2m25 円と4m50円は同じと分かることが大切である。省察では、今後の学習の見通しを考えさせたい。このような数学的活動を目指したい。
2人に共通すること 「単位を決める」
教科目標の柱書の視点から授業を考えていくことが大切である。子どもたちは、どんな眼鏡をかけてほしいと先生が願っているか。育てたい数学らしい眼鏡は何だったかを常日頃考えたい。自分で単位を決めること。両方とも扱った内容は違ったけど、根底にあるのは比例が前提である。










